Sign Test
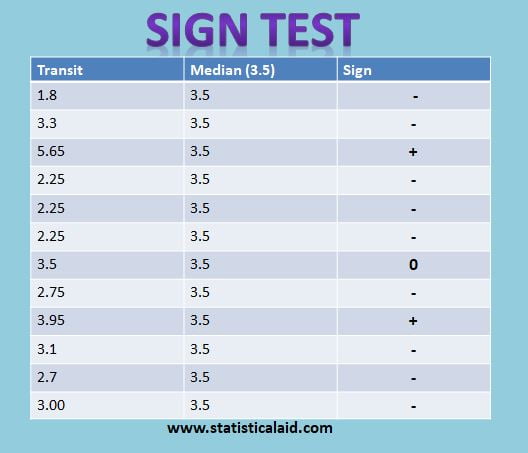
The sign test is the oldest of all non-parametric tests. and it is so called as usually covert the data for analysis to a series of plus and minus sign. The test statistic consists of either the number of plus sign or the number of minus sign.
Let,
x1,x2,......... xn be a random sample of size n from a N population with mean μ.
Sign test for small sample case (n< 35)
Assumptions of sign test
- The population is continuous and symmetric about mean.
- xi’s are independent.
Hypothesis of sign test
We want to test the following hypothesis.
1. 
Test
Procedure of sign test
Since,
the population is symmetric about μ. Then the
probability of sample value exceeding the mean μ and the
probability of a sample value less than μ are both
1/2 , get the difference, (xi-μ0); i=1,2,...,n. Put (t)
sign if (xi-μ0) > 0 and minus sign if (xi-μ0) < 0 for some i. If, (xi-μ0)=0 then simply
discard it from the analysis and n is reduced accordingly. Note that under H0,
the number of plus sign is binomial variance with index n and parameter θ=1/2.
Conclusion: If the observed number of plus sign falls in the critical region, we may reject our Ho. otherwise we may accept ho.
Sign test for large sample (n>35)
For large sample H0 may be test by,
Where, z is approximately normally distributed with mean 0 and variance 1. The approximation to the normal distribution becomes better if a correction for continuity is used. The correction is necessary since the normal distribution is continuous while the normal distribution is involved discrete variable. The corrected 2 becomes.
Comment: If the calculated value of z falls in
the critical region then we may reject our H0 otherwise accept our H0.
0 Comments