Random Variable and its Types with Properties

Random variables are a fundamental concept in probability and statistics, widely used in data analysis, machine learning, and various scientific disciplines. In this article, we will explore what a random variable is, its types, properties, and applications.

In statistics, A Random Variable is a set of possible values from a random experiment which is known in advance and the experiment can be repeated under identical conditions. According to Investopedia, “A random variable is a variable whose value is unknown or a function that assigns values to each of an experiment’s outcomes.”

A random experiment is an experiment in which

• The experimenter knows all possible outcomes in advance.
• The experiment produces an outcome that is not exactly known beforehand.
• The experimenter can repeat the experiment under identical conditions.

More precisely we can say that,

A rule assigns a real number to each outcome (sample point) of a random experiment, defining a random variable (r.v.). A function of the variable governs it. Hence, it is a real-valued function X (x) of the elements of the simple space (omega) where x is an element of (omega). Further, the range of the variable will be a set of real values. 

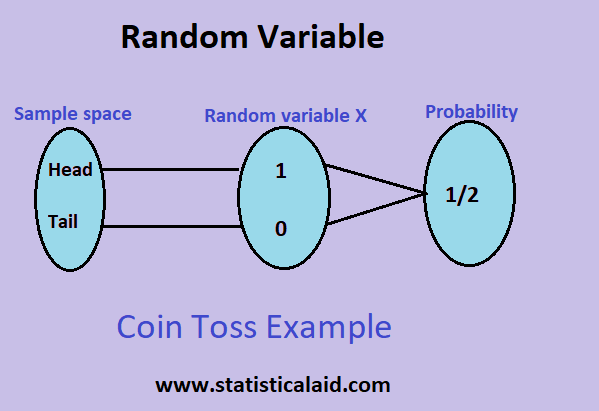
For example, In tossing a coin, x =1, if the coin falls with head, and x= 0 if the coin falls with a tail. The height of persons can be given by X (x)= X, the height is measured in centimeters or inches. We usually denote a random variable by any of the capital Latin letters X, Y, Z, U, V, etc.

Types of Random Variables

Random variables can be classified into two main types:

1. Discrete Random Variables: These variables take on a finite or countable number of values. Examples include the number of heads in a series of coin tosses or the number of defective items in a batch.
   • Example: Rolling a six-sided die (values: 1, 2, 3, 4, 5, 6). Say, x is a variable, which can take a finite number of values in an interval of the domain, is called a discrete random variable. For example, if we toss a coin, the variable can take only two values 0 and 1 assigned to tail and head respectively, i.e., X(x)= 0(if x is tail) or 1(if x is head).
2. Continuous Random Variables: These variables take an infinite number of values within a given range. Examples include the height of students in a class or the time required to complete a task.
   • Example: The temperature in a city on a given day (values can be any real number within a range). Let, A variable X, which can take any value in its domain or in an interval or the union of intervals on the real line, is called continuous random variable. For a conti­nuous variable, the probability of a point is zero, i.e., P (X = x) =0.

Probability Distribution of Random Variables

A probability distribution describes how likely different values of a random variable are to occur. There are two key types:

1. Probability Mass Function (PMF): Used for discrete random variables, the PMF gives the probability of each possible value occurring.
2. Probability Density Function (PDF): Used for continuous random variables, the PDF represents the likelihood of values within an interval occurring.

Another essential concept is the Cumulative Distribution Function (CDF), which provides the probability that a random variable takes a value less than or equal to a given number.

Properties of Random Variable

The properties are following,

• If X is a variable and a, b are any two constants, aX + b is also a random variable.
• If X is a variable, X square is also a variable.
• If X is a variable, 1/X is also a variable.
• If X and Y are two variables defined over the same space, X + Y, X -Y, aX, bY or aX + by are also random variables where a and b are any two constants except that a and b both are not zero.

Applications of Random Variables

Random variables are widely used in various fields, including:

• Finance: Modeling stock prices and risk analysis.
• Machine Learning: Used in probabilistic models and Bayesian inference.
• Engineering: Reliability testing and quality control.
• Medicine: Analyzing patient recovery times and drug effectiveness.

Understanding random variables is crucial for working with probability and statistics. Whether discrete or continuous, these variables help us quantify uncertainty and make data-driven decisions. By mastering their properties and distributions, you can enhance your analytical skills and apply them across multiple domains.