Statistical Aid: A School of Statistics
Learn Statistics and Data Analysis Intuitively!
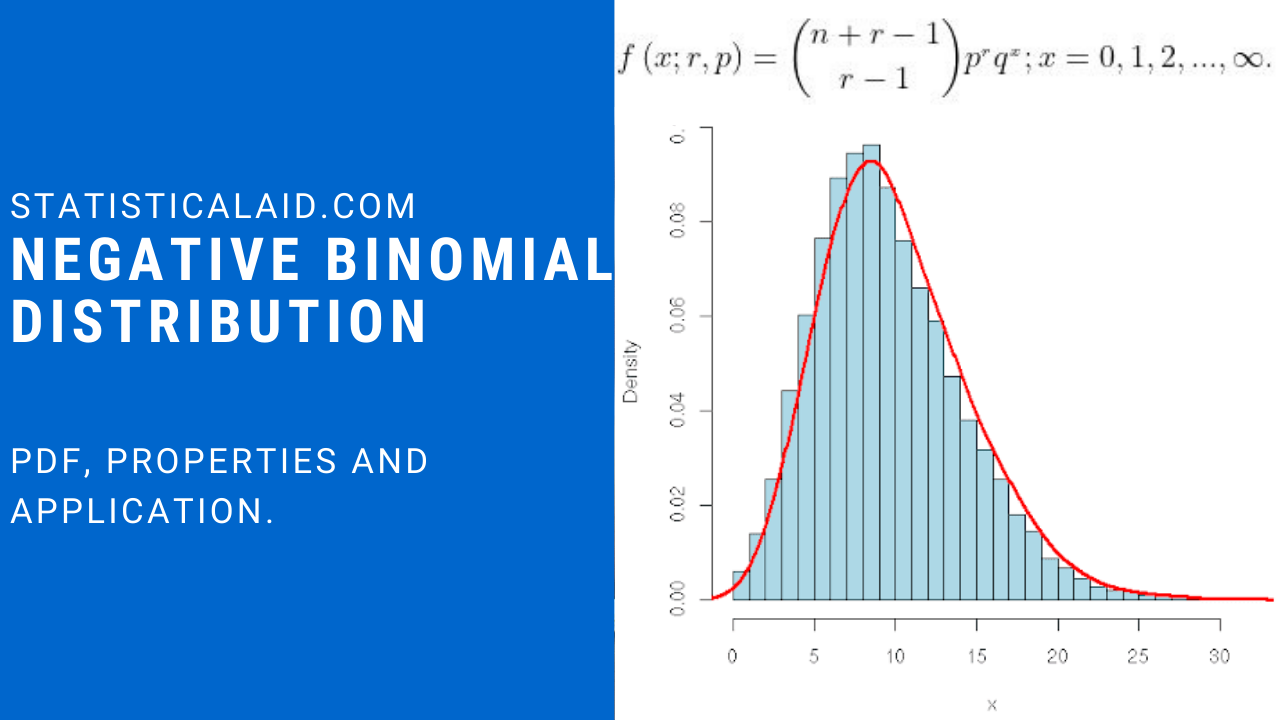
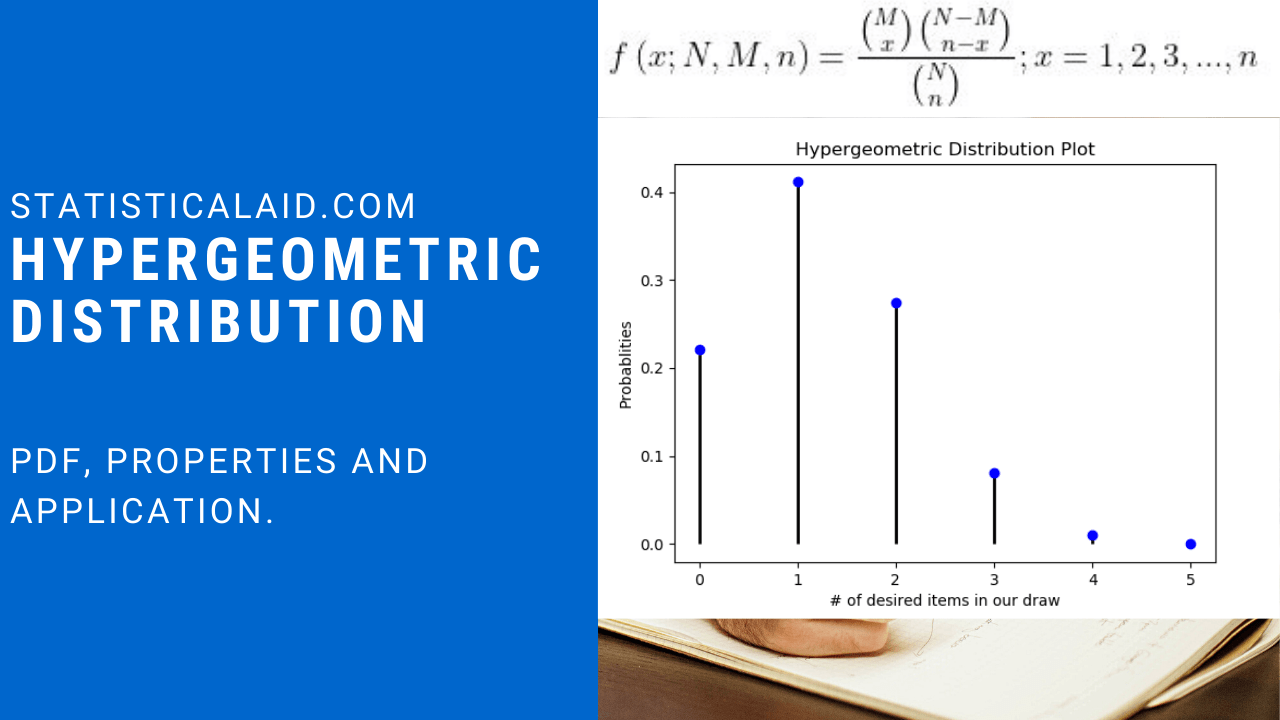
The Weibull distribution is a cornerstone of probability and statistics, renowned for its flexibility and wide range of applications. Whether you’re an engineer analyzing the reliability of machine parts, a statistician modeling life data, or a data scientist working with time-to-event data, the Weibull distribution offers a powerful framework for understanding and predicting outcomes. In … Read more
In the world of statistics, we often talk about distributions. A distribution, at its core, is simply a way to show how often different values occur within a dataset. While many introductory statistics lessons focus on the perfectly symmetrical and beautiful Normal Distribution (also known as the Bell Curve), the reality is that much of … Read more
In the fascinating world of statistics, we often encounter data that clusters around a central tendency, like the familiar bell curve of a normal distribution. But what happens when the data seems to have two centers, showing two distinct peaks? This is where the bimodal distribution comes in. While less common than its unimodal cousin, … Read more
In statistics, probability distributions are a very important measure that relates to the random variable and statistical data. Every data pattern follows a probability distribution. Continuous data follow a continuous distribution, and discrete data follow discrete distributions. According to Wikipedia, “In probability theory and statistics, a probability distribution is the mathematical function that gives the … Read more
In probabilistic statistics, the gamma distribution is a two-parameter family of continuous probability distributions which is widely used in different sectors. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of it. Gamma distribution is a crucial concept in probability theory and statistics, widely used in various scientific fields such as finance, engineering, … Read more
In probabilistic statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process where events occur continuously and independently at a constant average rate. It is a special case of the gamma distribution. The exponential distribution is frequently used to calculate the amount of time until a certain … Read more
Uniform distribution is a fundamental concept in probability theory and statistics. It represents a scenario where all outcomes are equally likely, making it an essential tool in data analysis, simulations, and real-world applications. It is used in statistics to describe a type of probability distribution in which every conceivable outcome has an equal chance of … Read more
A power series distribution is a discrete probability distribution that applies to a subset of natural numbers. The distribution’s names derive from the fact that the power series is used to construct them. This broad category of distributions includes a number of discrete distributions, such as the Poisson distribution, negative binomial distribution, and binomial distribution. … Read more
The logarithmic series distribution is a discrete probability distribution obtained from the Maclaurin series expansion. Sometimes it is known as log-series distribution. It has a long right tail with one parameter, which ranges from 0 to 1. This distribution models a wide range of events, including data on animal diversity and the frequency of insurance … Read more
The Negative Binomial Distribution (NBD) is a crucial probability distribution in statistics, especially in modeling count data with overdispersion. It is widely applied in fields such as epidemiology, finance, and machine learning. This article provides an in-depth exploration of the NBD, its formula, applications, and real-world significance. What is the Negative Binomial Distribution? The Negative … Read more
You cannot copy content of this page