The Wilcoxon signed rank test determine whether the median of the sample is equal to some specified value. It utilizes both the sign of the difference as well as the magnitude of the differences, hence it provides more information than the sign test, it is often more powerful non-parametric test.
The Wilcoxon Signed-Rank Test is a non-parametric statistical test used to compare two related samples. It is an alternative to the paired t-test when the data does not meet the normality assumption. This test is widely used in research fields such as medicine, psychology, and economics to analyze paired or matched data.
Assumptions Wilcoxon Signed ranked test
- The population from which the sample is drawn is symmetric.
- The observations are independent.
- The scale of measurement is at least interval.
- Data are paired and come from the same population.
- Each pair is chosen randomly.
When to Use the Wilcoxon Signed-Rank Test
The Wilcoxon Signed-Rank Test is appropriate when:
- The data is paired or dependent (e.g., before-and-after measurements).
- The differences between paired observations are not normally distributed.
- The measurement scale is at least ordinal.
Hypothesis of Wilcoxon Signed ranked test
We want to test the following hypothesis :
Test Procedure
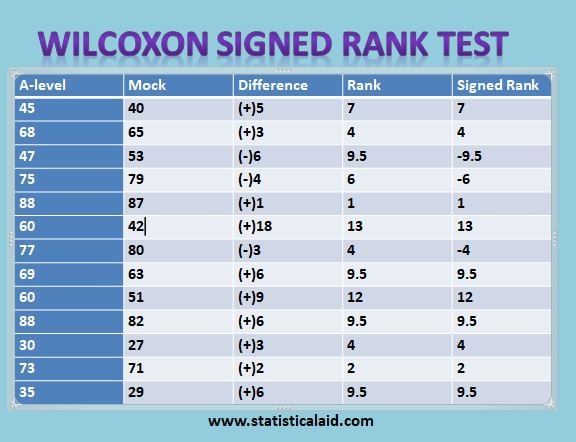
Firstly we find the difference,
Critical Region and Comment
Wilcoxon Signed Rank Test for large sample (n >25)
Comment: If the calculated vale of z falls in the critical region then we may reject our null hypothesis /H0 ; Otherwise we may accept it.
How to perform the test?
Let, we have two scores: math score and physics score.
Step-1: Subtract physics score from math score to get the differences:
Step-2: place the differences in order and then rank them. Ignore the sign when placing in rank order.
Step-3: Note the sign of the difference.
Step-4: Calculate the sum of the ranks of the negative differences (W– ).
Step-5: Calculate the sum of the ranks of the positive differences (W+ ).
And Finally, follow the above test procedure to find the result.
Interpretation of Results
- Reject the Null Hypothesis (H₀): There is a significant difference between the two paired samples.
- Fail to Reject H₀: There is no significant difference between the two paired samples.
Example Application of Wilcoxon Signed Rank Test
Suppose a researcher wants to determine if a new drug improves reaction times. They measure reaction times before and after administering the drug to 10 participants. If the data does not follow a normal distribution, the Wilcoxon Signed-Rank Test can be used to determine if there is a significant difference in reaction times.
Advantages and Disadvantages
Advantages:
- Works for non-normally distributed data.
- Suitable for small sample sizes.
- More robust than the paired t-test.
Limitations of Wilcoxon Signed Rank Test
According to Wikipedia, there are some limitation of Wilcoxon signed rank test. They are: when the difference between the groups is zero, the observations are discarded. This is of particular concern if the samples are taken from a discrete distribution. In these scenarios the modification to the Wilcoxon test by Pratt 1959, provides an alternative which incorporates the zero differences. This modification is more robust for data on an ordinal scale.
See other non-parametric Test:
The Wilcoxon Signed Rank Test is a valuable tool for analyzing paired data without assuming normality. It is widely used in various scientific disciplines to assess treatment effects, behavior changes, and performance improvements. Machine Learning