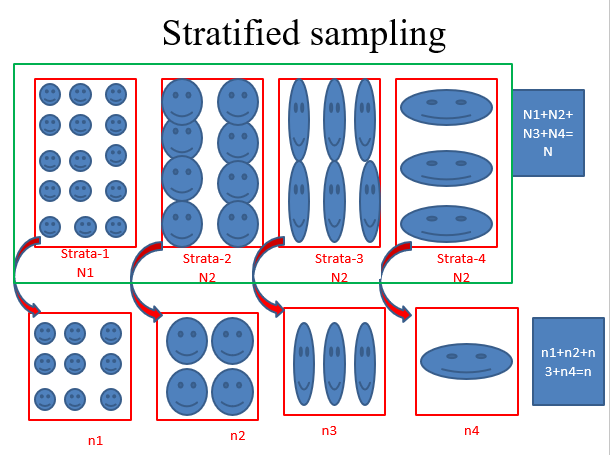
Stratified sampling: Allocation rules with advantages and disadvantages

Stratified sampling is a sampling plan in which we divide the population into several non-overlapping strata and select a random sample from each stratum in such a way that units within the strata are homogeneous but between strata they are heterogeneous. Stratum is a group of elements where all the units of elements “within the strata are homogeneous but between strata they are heterogeneous”. Homogeneous means alike or contains same characteristics and heterogeneous means different from each other or contains different characteristics. [Note: ‘Stratum’ is a singular form and ‘strata’ is a plural form].
Stratified sampling is a probability sampling.

What is Stratified Sampling?

Stratified sampling begins by partitioning the population into mutually exclusive and collectively exhaustive strata, such as age groups, income levels, or geographic regions, where each stratum shares similar traits. Researchers then draw random samples from each stratum, often proportionally to the stratum’s size in the population, ensuring the sample mirrors the population’s diversity. This approach enhances representativeness, as it prevents under- or over-sampling of important subgroups that might occur in simpler methods.

The core principle relies on homogeneity within strata and heterogeneity between them, which minimizes variance and boosts statistical efficiency. For instance, in a national health survey, strata might include urban vs. rural residents, allowing targeted insights into each group’s health patterns without bias.

Types of Stratified Sampling

Stratified sampling varies by allocation strategy:

Proportionate Stratified Sampling: Sample sizes from each stratum match their proportion in the population, preserving overall structure for unbiased population estimates.
Disproportionate Stratified Sampling: Oversamples smaller or rarer strata to improve precision for those groups, then weights results during analysis.
Optimal Allocation: Adjusts sample sizes based on stratum variance and cost, balancing accuracy and efficiency.

These types allow flexibility for different research needs, from general population studies to focused subgroup analysis.

How to Conduct Stratified Sampling

Implementing stratified sampling follows these structured steps:

Identify key stratifying variables like demographics or behaviors that influence the outcome.
Obtain a sampling frame with population data to define and size strata accurately.
Calculate sample sizes per stratum, using formulas like n_h = N_h/N × n for proportionate allocation, where n_h is the stratum sample, N_h its population size, N total population, and n total sample.
Randomly select individuals from each stratum using tools like random number generators.
Collect data and apply weights if disproportionate sampling was used.

Software such as R, Python’s pandas, or survey platforms automates this process for large datasets.

Allocation rules of stratified sampling

Equal allocation
Proportional allocation
Neyman allocation
Optimum allocation

Equal Allocation

In equal allocation we have to divide the sample size(n) by the number of strata.

Proportional allocation

In proportional allocation we have divide the sample size(n) by the total smple size(N) and multiply with stratum size(Ni).

Neyman or optimal allocation

Neyman allocation is a special case of optimal allocation.

Advantages of stratified sampling

Stratification tends to decrease the variance of the sample estimates. This result is smaller bound on the error of estimation. This is particularly true if measurements within strata are homogeneous.
By stratification, the cost per observation in the survey may be reduced by the stratification of the population elements into convenient groupings.
When separate estimates for population parameters for each sub-population within an overall population is required, stratification is rewarding.
Stratification makes it possible to use different sampling designs in different strata.
Stratification is particularly more effective when there are extrem values in the population, which can be segregated into separate strata. Thereby reducing the variability within strata.
It is most effective in handling the heterogenous population.
In stratified sampling, confidence intervals may be constructed individually for the parameter of interest in each stratum.

Disadvantages of stratified sampling

The major disadvantages are that it may take more time to select the sample than would be the case for simple random sampling. More time is involved because complete frames are necessary within each of the strata and each stratum must be sampled. There are some other disadvantages of stratified sampling-

It requires more administrative works as compared with Simple Random Sampling.
It is sometimes hard to classify each kind of population into clearly distinguished classes.
It can be tedious and time consuming job to those who are not keen towards handling such data.

Real-World Examples and Applications

Stratified sampling shines in practical scenarios:

Market Research: A consumer goods company divides customers by income strata to test product preferences proportionally, revealing segment-specific demands.
Public Health: During a disease outbreak, health officials stratify by age and region to sample vaccination rates accurately across vulnerable groups.
Education: Schools stratify students by grade level and performance tiers to evaluate teaching interventions’ impact per subgroup.
Environmental Studies: Ecologists sample wildlife by habitat strata (forest, wetland) to estimate species diversity without underrepresenting sparse areas.

In elections, pollsters use it to balance demographics like race and education, improving prediction accuracy.

Comparison with Other Sampling Methods

Method	Key Feature	Best For	Drawback
Simple Random	Equal chance for all	Homogeneous populations	Misses subgroups in diverse groups
Stratified	Proportional strata representation	Heterogeneous populations	Needs strata data
Cluster	Groups as units	Geographically dispersed	Higher error if clusters similar
Systematic	Fixed intervals	Ordered lists	Risk of periodicity bias

Stratified often outperforms others in precision for varied populations.

Conclusion

Stratified sampling stands as a powerful tool for achieving representative, precise samples in complex populations by thoughtfully dividing groups and sampling proportionally. Its ability to highlight subgroup differences while minimizing error makes it indispensable for credible research outcomes. Despite data requirements, its advantages in efficiency and accuracy drive its use across industries, fostering better-informed decisions. Data Science Blog

Q&A

Q: When should stratified sampling be used over simple random sampling?
A: Use it for heterogeneous populations where subgroups matter, to ensure representation and reduce error.

Q: What makes strata effective in stratified sampling?
A: Strata should be internally homogeneous and mutually exclusive, capturing key variations.

Q: How do you handle disproportionate stratified sampling?
A: Weight samples inversely to their oversampling during analysis for unbiased estimates.

Q: Is stratified sampling always more accurate?
A: Yes, when strata are well-defined; otherwise, it risks misclassification bias.

Q: What software supports stratified sampling?
A: Tools like R’s survey package, Python’s stratified_shuffle_split, or Qualtrics streamline it.