Negative Binomial Distribution definition, properties with application

The Negative Binomial Distribution (NBD) is a crucial probability distribution in statistics, especially in modeling count data with overdispersion. It is widely applied in fields such as epidemiology, finance, and machine learning. This article provides an in-depth exploration of the NBD, its formula, applications, and real-world significance.

What is the Negative Binomial Distribution?

The Negative Binomial Distribution (NBD) describes the probability of observing a fixed number of failures before achieving a predefined number of successes in a series of independent Bernoulli trials. Unlike the binomial distribution, which models the number of successes in a fixed number of trials, NBD focuses on the number of trials needed to reach a given number of successes.

In a negative binomial experiment, a negative binomial random variable is the number X of repeated trials required to obtain r successes. A NBD is the probability distribution of a negative binomial random variable. The Pascal distribution is another name for the negative binomial distribution. According to Wikipedia, The distribution of the number of trials required in an experiment to attain a specific number of successes was originally investigated in 1713 by Montmort. Pascal has previously mentioned this.

Negative Binomial Distribution Formula

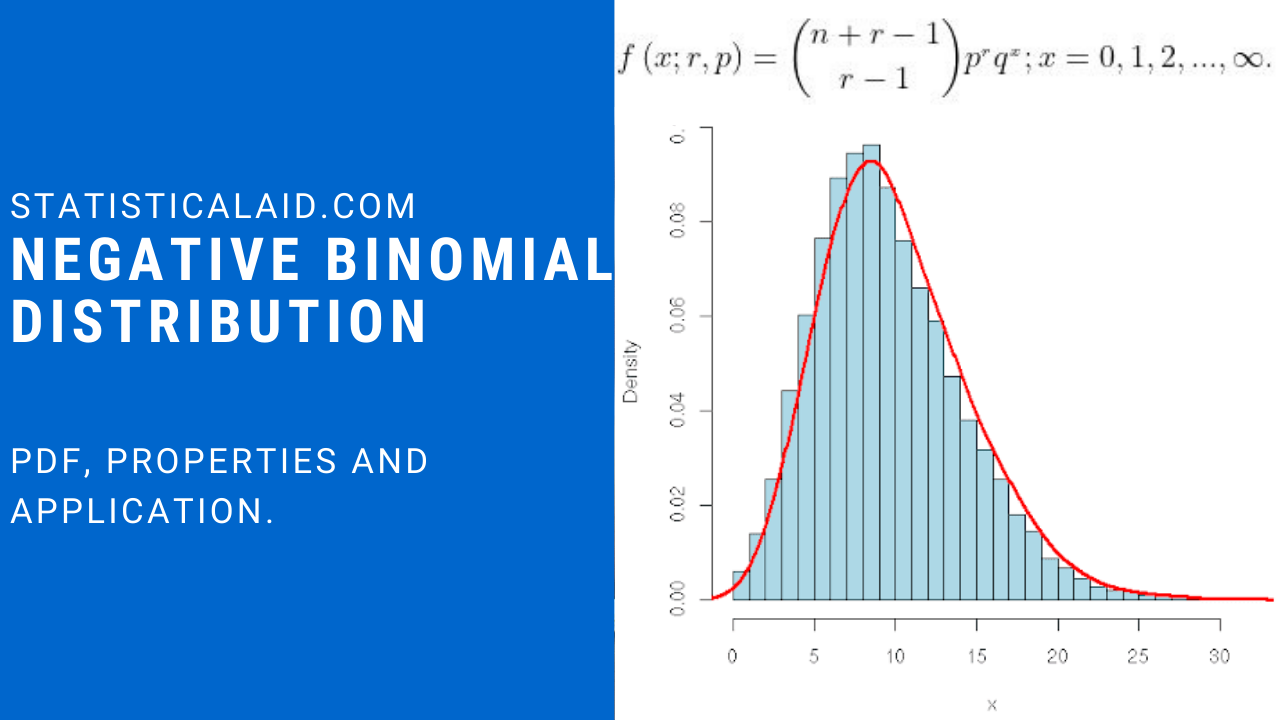
A discrete random variable X is said to have Negative binomial distribution if its probability density function is defined as,

$f(x;r,p)=(_{r-1}^{n+r-1})p^{r}q^{x}; x=0,1,2,...,\infty$

Where r>0 and 0<=p<=1 are the two parameter of the distribution such that p+q=1. f(x;r,p) is the probability of getting exactly r successes in (x+r) independent Bernoulli trials.

Assume we repeatedly flip a coin and count the number of heads (successes). We’re performing a negative binomial experiment if we keep flipping the coin till it lands on heads two times. The number of coin flips required to acquire two heads is the negative binomial random variable. The number of coin flips is a random variable in this example, and it can have any integer value between 2 and infinity.

Key Assumptions:

Each trial results in either a success or a failure.
The probability of success remains constant for all trials.
Trials are independent of each other.

Properties of Negative Binomial Distribution

The mean of negative binomial distribution is ${frac {pr}{1-p}}$ .
The variance of the distribution is ${frac {pr}{(1-p)^{2}}}$ .
The skewness of the distribution is ${frac {1+p}{sqrt {pr}}}$ .
The kurtosis of negative binomial distribution is ${frac {6}{r}}+{frac {(1-p)^{2}}{pr}}$ .

Characteristics

Some characteristics of negative binomial is given below-

If r=1, negative binomial distribution tends to geometric distribution with parameter p.
If r➝∞, q➝0 and rq➝λ, then NBD tends to Poisson distribution.
The variance of negative binomial distribution is always greater than mean.
The distribution is positively skewed and leptokurtic.

Special Cases

Geometric Distribution: When, the negative binomial distribution simplifies to the geometric distribution, which models the number of failures before the first success.
Poisson-Gamma Mixture: The NBD can be viewed as a Poisson distribution with a gamma-distributed mean, making it suitable for modeling overdispersed Poisson data.

Applications

1. Epidemiology: Used to model the number of infections before a certain number of recoveries, particularly in the spread of diseases.

2. Insurance and Risk Management: Applied in claims modeling, where insurance claims are overdispersed and do not fit the Poisson distribution.

3. Marketing and Consumer Behavior: Used to model customer purchases and repeat transactions, particularly in lifetime value analysis.

4. Machine Learning and NLP: Applied in natural language processing (NLP) to model word frequency distributions in text data.

Difference Between Negative Binomial and Binomial Distributions

Feature	Binomial Distribution	Negative Binomial Distribution
Fixed Value	Fixed number of trials (n)	Fixed number of successes (r)
Variable	Number of successes	Number of failures
Common Use	Success probability estimation	Overdispersed count modeling

Conclusion

The Negative Binomial Distribution is a powerful statistical tool for modeling overdispersed count data. With applications spanning various fields, understanding its properties, formula, and real-world implications can help statisticians and data scientists make informed decisions.

By leveraging the NBD, analysts can effectively model and interpret data that does not conform to simpler distributions like the binomial or Poisson.